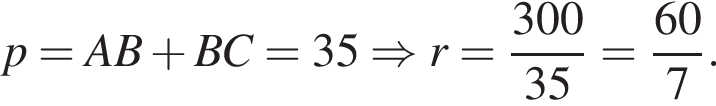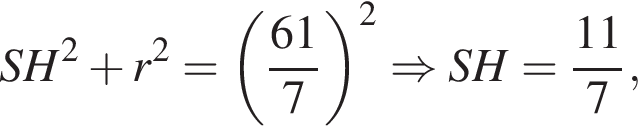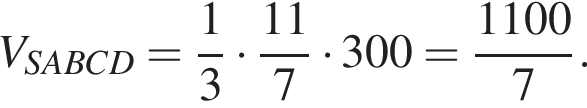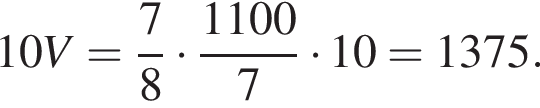Определите наименьшее натуральное число, кратное 2, которое при делении на 15 с остатком дает неполное частное, равное 3.
Выразите 737 см 8 мм в метрах с точностью до сотых.
Сумма всех натуральных делителей числа 28 равна:
Значение выражения 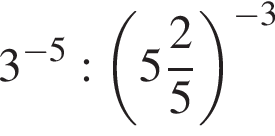 равно:
равно:
Если 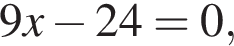 то
то 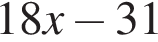 равно:
равно:
Найдите значение выражения 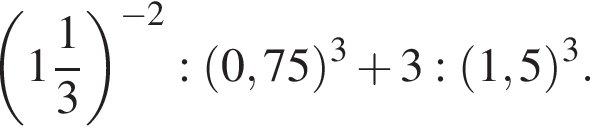
Решите неравенство 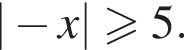
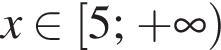


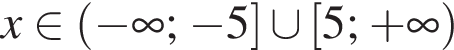
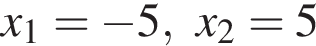
Запишите формулу n-го члена арифметической прогрессии (an), если даны ее первые пять членов: −10, −4, 2, 8, 14.
Площадь круга равна ![]() Диаметр этого круга равен:
Диаметр этого круга равен:
Значение выражения 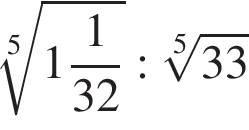 равно:
равно:
Даны два числа. Известно, что одно из них меньше другого на 6. Какому условию удовлетворяет меньшее число x, если его удвоенный квадрат не больше суммы квадратов этих чисел?


На одной чаше уравновешенных весов лежат 3 яблока и 1 груша, на другой — 2 яблока, 2 груши и гирька весом 20 г. Каков вес одного яблока (в граммах), если все фрукты вместе весят 780 г? Считайте все яблоки одинаковыми по весу и все груши одинаковыми по весу.
Значение выражения НОК(18, 20, 45) + НОД(30, 42) равно:
Известно, что наименьшее значение функции, заданной формулой y = x2 + 8x + c, равно −5. Тогда значение c равно:
Найдите сумму целых решений неравенства 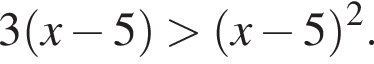
Расположите числа 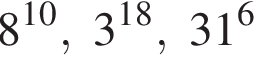 в порядке возрастания.
в порядке возрастания.
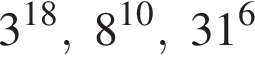
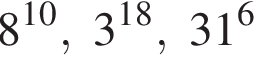
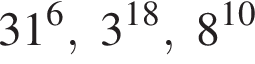
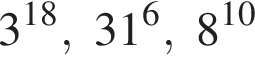
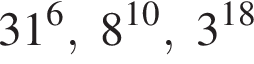
Через вершину A прямоугольного треугольника ABC (∠C = 90°) проведен перпендикуляр AK к его плоскости. Найдите расстояние от точки K до прямой BC, если AK = 2, AB = 4, BC = ![]()
Наименьшее целое решение неравенства 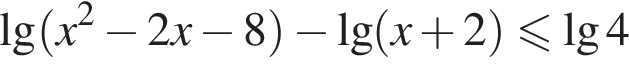 равно:
равно:
Для начала каждого из предложений A−В подберите его окончание 1−6 так, чтобы получилось верное утверждение.
A) Окружность с центром в точке (−8; −2) и радиусом 4 задается уравнением:
Б) Уравнением прямой, проходящей через точку (−8; 2) и параллельной прямой 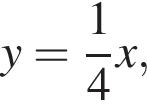 имеет вид:
имеет вид:
В) График обратной пропорциональности, проходящий через точку 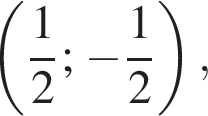 задается уравнением:
задается уравнением:
1) ![]()
2) 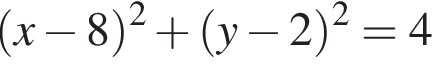
3) 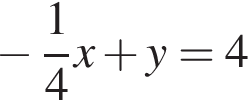
4) 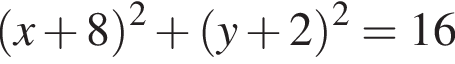
5) 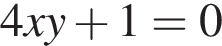
6) 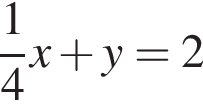
Ответ запишите в виде сочетания букв и цифр, соблюдая алфавитную последовательность букв левого столбца. Помните, что некоторые данные правого столбца могут использоваться несколько раз или не использоваться вообще. Например: А1Б1В4.
Внутренний угол правильного многоугольника равен 135°. Выберите все верные утверждения для данного многоугольника.
1. Многоугольник является восьмиугольником.
2. В многоугольнике 40 диагоналей.
3. Если сторона многоугольника равна 2, то радиус вписанной окружности равен 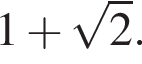
4. Площадь многоугольника со стороной a можно вычислить по формуле 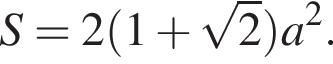
Ответ запишите в виде последовательности цифр в порядке возрастания. Например: 123.
В равнобедренную трапецию, площадь которой равна ![]() вписана окружность. Сумма двух углов трапеции равна 60°. Найдите периметр трапеции.
вписана окружность. Сумма двух углов трапеции равна 60°. Найдите периметр трапеции.
Найдите произведение корней (корень, если он единственный) уравнения 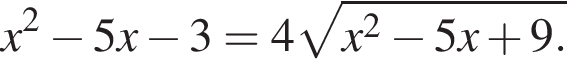
Найдите сумму (в градусах) наименьшего положительного и наибольшего отрицательного корней уравнения 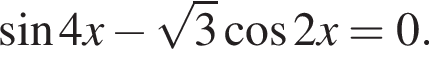
Три числа составляют геометрическую прогрессию, в которой ![]() Если второй член прогрессии уменьшить на 8, то полученные три числа в том же порядке опять составят геометрическую прогрессию. Если третий член новой прогрессии уменьшить на 25, то полученные числа составят арифметическую прогрессию. Найдите сумму исходных чисел.
Если второй член прогрессии уменьшить на 8, то полученные три числа в том же порядке опять составят геометрическую прогрессию. Если третий член новой прогрессии уменьшить на 25, то полученные числа составят арифметическую прогрессию. Найдите сумму исходных чисел.
Найдите сумму целых решений неравенства 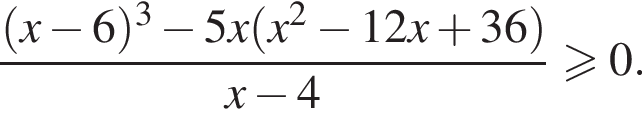
Найдите сумму наименьшего и наибольшего целых решений неравенства 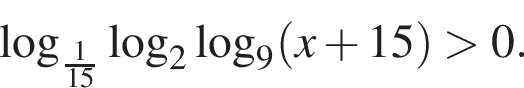
В арифметической прогрессии 130 членов, их сумма равна 130, а сумма членов с четными номерами на 130 больше суммы членов с нечетными номерами. Найдите сотый член этой прогрессии.
Найдите произведение наибольшего целого решения на количество целых решений неравенства 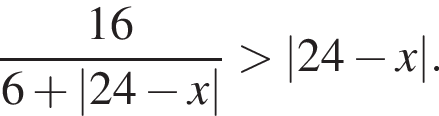
Из двух растворов с различным процентным содержанием спирта массой 100 г и 900 г отлили по одинаковому количеству раствора. Каждый из отлитых растворов долили в остаток другого раствора, после чего процентное содержание спирта в обоих растворах стало одинаковым. Найдите, сколько раствора (в граммах) было отлито из каждого раствора.
Трое рабочих (не все одинаковой квалификации) выполнили некоторую работу, работая поочередно. Сначала первый из них проработал ![]() часть времени, необходимого двум другим для выполнения всей работы. Затем второй проработал
часть времени, необходимого двум другим для выполнения всей работы. Затем второй проработал ![]() часть времени, необходимого двум другим для выполнения всей работы. И, наконец, третий проработал
часть времени, необходимого двум другим для выполнения всей работы. И, наконец, третий проработал ![]() часть времени, необходимого двум другим для выполнения всей работы. Во сколько раз быстрее работа была бы выполнена, если бы трое рабочих работали одновременно? В ответ запишите найденное число, умноженное на 4.
часть времени, необходимого двум другим для выполнения всей работы. Во сколько раз быстрее работа была бы выполнена, если бы трое рабочих работали одновременно? В ответ запишите найденное число, умноженное на 4.
Петя записал на доске два различных натуральных числа. Затем он их сложил, перемножил, вычел из большего записанного числа меньшее и разделил большее на меньшее. Сложив четыре полученных результата, Петя получил число 1521. Найдите все такие пары натуральных чисел. В ответ запишите их сумму.
Основанием пирамиды SABCD является выпуклый четырехугольник ABCD, диагонали АС и BD которого перпендикулярны и пересекаются в точке O, АО = 9, ОС = 16, ВО = OD = 12. Вершина S пирамиды SABCD удалена на расстояние ![]() от каждой из прямых AB, BC, СD и AD. Через середину высоты пирамиды SABCD параллельно ее основанию проведена секущая плоскость, которая делит пирамиду на две части. Найдите значение выражения 10 · V, где V — объем большей из частей.
от каждой из прямых AB, BC, СD и AD. Через середину высоты пирамиды SABCD параллельно ее основанию проведена секущая плоскость, которая делит пирамиду на две части. Найдите значение выражения 10 · V, где V — объем большей из частей.

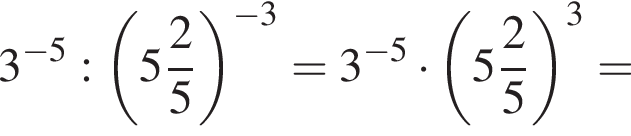
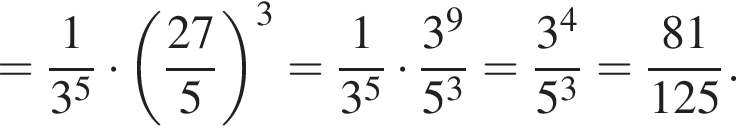
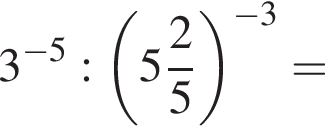
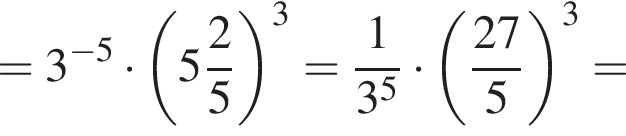
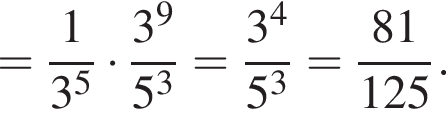
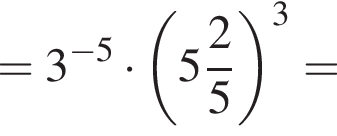
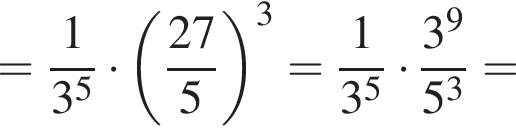
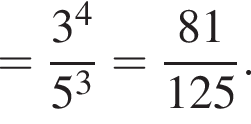
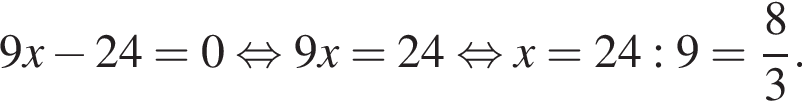
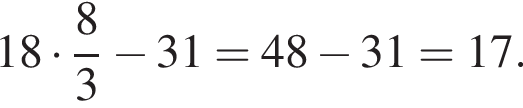
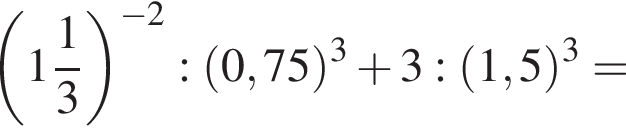

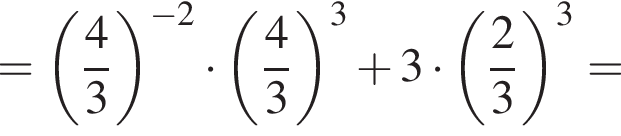
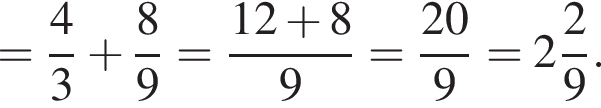
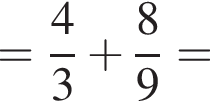
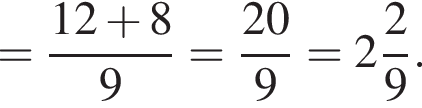

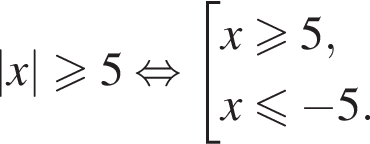
 имеем:
имеем: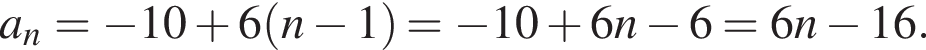
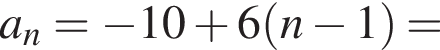

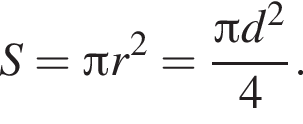 Следовательно,
Следовательно, 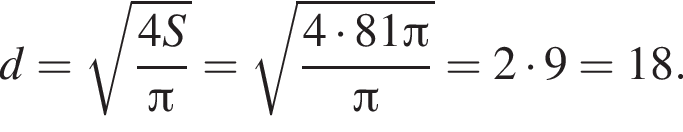
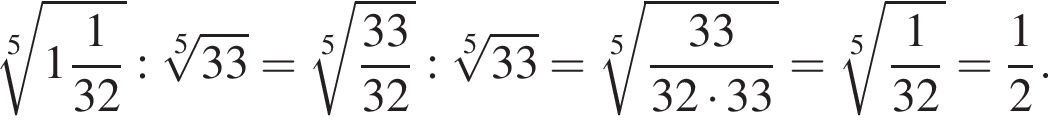
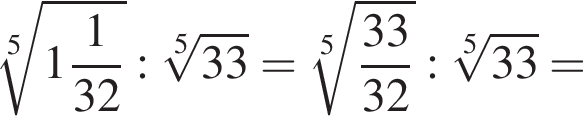
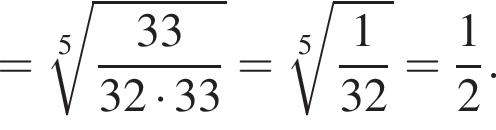
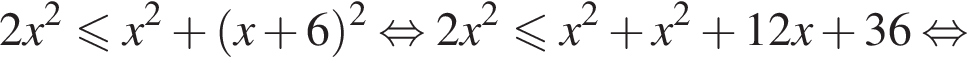

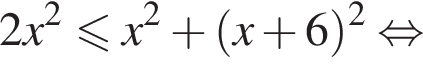
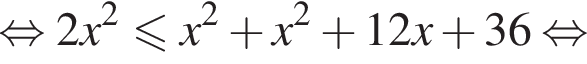
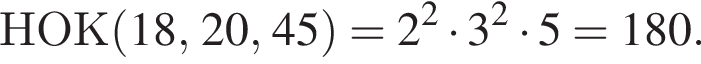
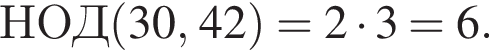 Поэтому сумма НОК(18, 20, 45) и НОД(30, 42) равна 18 + 6 = 186.
Поэтому сумма НОК(18, 20, 45) и НОД(30, 42) равна 18 + 6 = 186.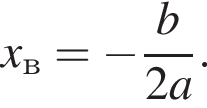 Поэтому
Поэтому 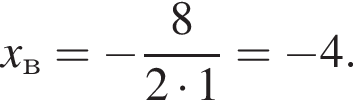 Поскольку y(xв) = −5, имеем:
Поскольку y(xв) = −5, имеем: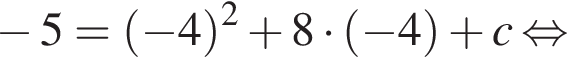

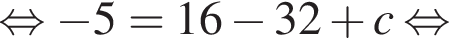
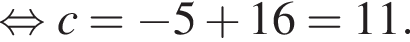
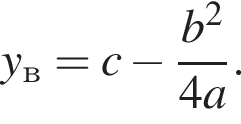
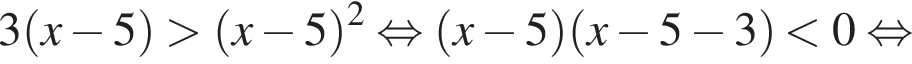

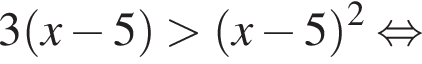
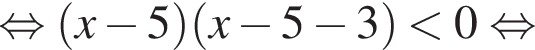
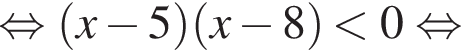

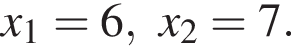 Их сумма равна:
Их сумма равна: 
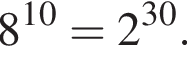 Поскольку все числа положительны, извлечем из каждого корень шестой степени и получим:
Поскольку все числа положительны, извлечем из каждого корень шестой степени и получим: 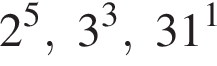 то есть числа 32, 27, 31. Так как 27 < 31 < 32, получаем
то есть числа 32, 27, 31. Так как 27 < 31 < 32, получаем 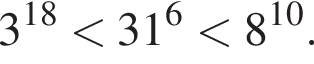
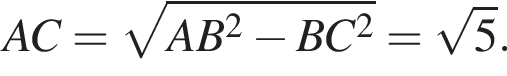 Заметим, что AC является проекцией наклонной KC на плоскость ABC и AC
Заметим, что AC является проекцией наклонной KC на плоскость ABC и AC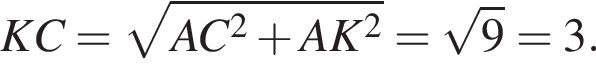
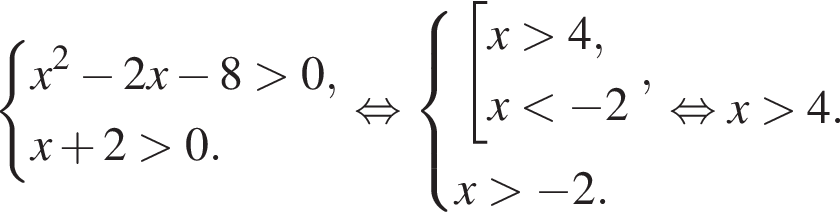
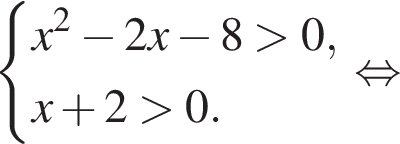
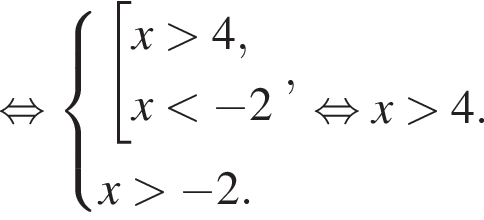
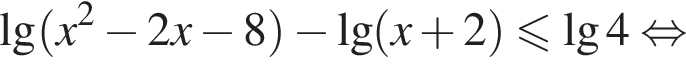
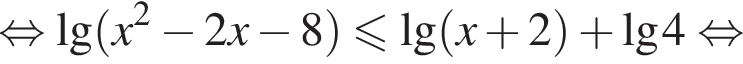
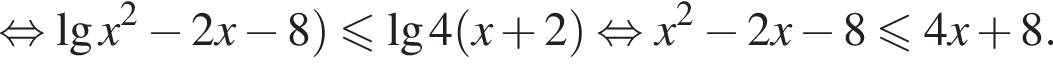
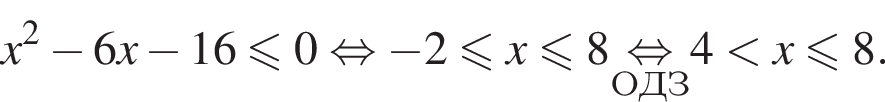
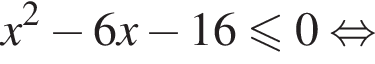
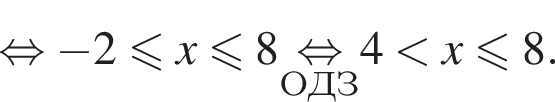
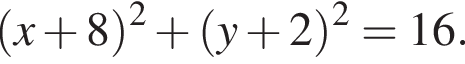
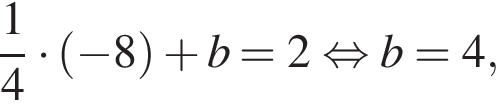 т. е.
т. е. 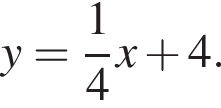
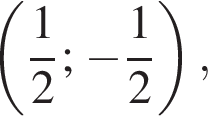 задается уравнением:
задается уравнением:  т. е.
т. е. 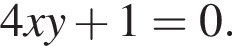
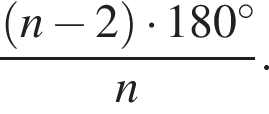 Тогда
Тогда 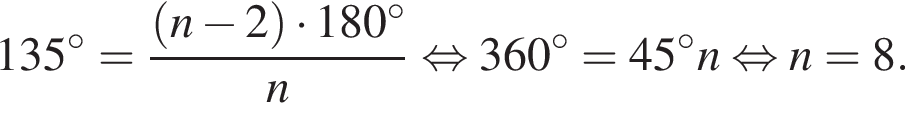
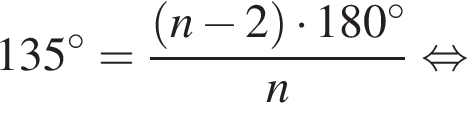
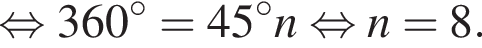
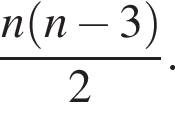 При n = 8, получаем, что диагоналей 20. Второе утверждение неверно.
При n = 8, получаем, что диагоналей 20. Второе утверждение неверно.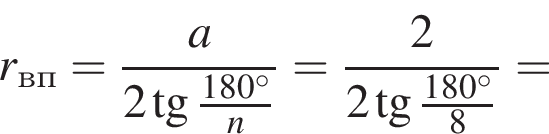
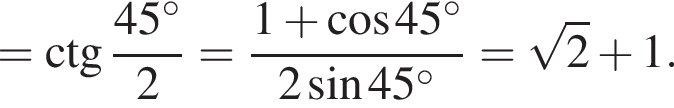
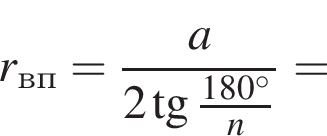
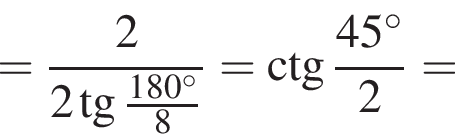
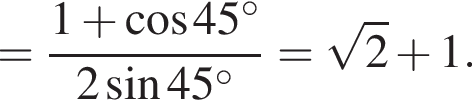
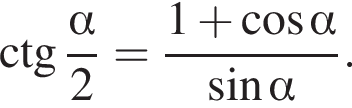
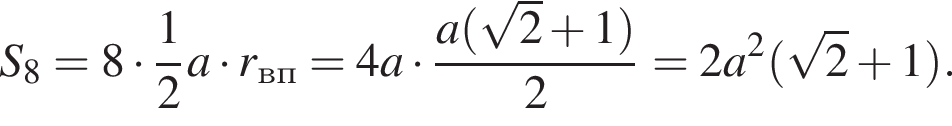
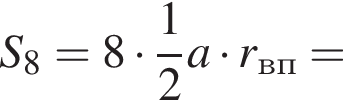
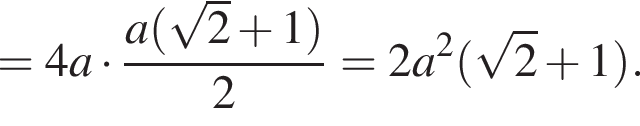
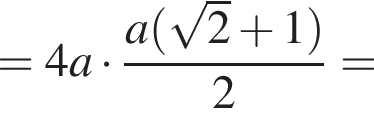
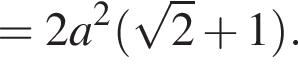
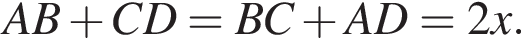 Сумма углов в равнобедренной трапеции, прилежащих к одной стороне равна 180°, откуда следует, что сумма углов, данная в условии — есть сумма углов при основании AD, которые равны.
Сумма углов в равнобедренной трапеции, прилежащих к одной стороне равна 180°, откуда следует, что сумма углов, данная в условии — есть сумма углов при основании AD, которые равны. 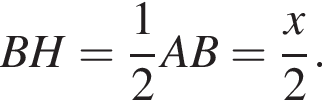 Поэтому из площади трапеции найдем x:
Поэтому из площади трапеции найдем x: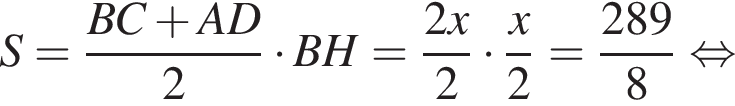
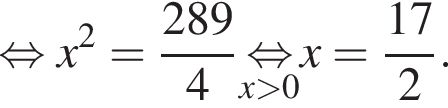
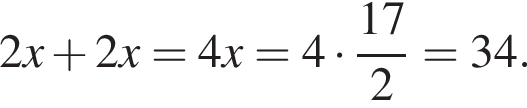
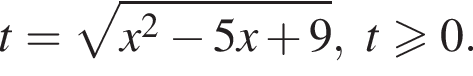 Имеем:
Имеем: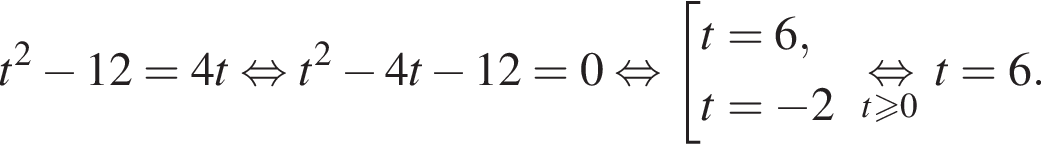
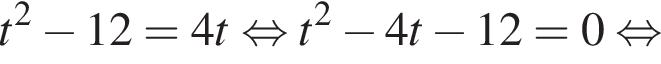
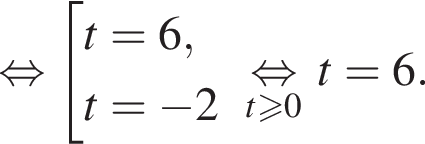

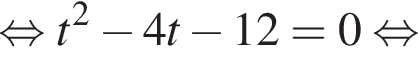
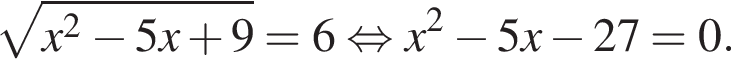 Полученное уравнение имеет один положительный и один отрицательный корень. Согласно теореме Виета, произведение корней уравнения равно −27.
Полученное уравнение имеет один положительный и один отрицательный корень. Согласно теореме Виета, произведение корней уравнения равно −27. Тогда:
Тогда:
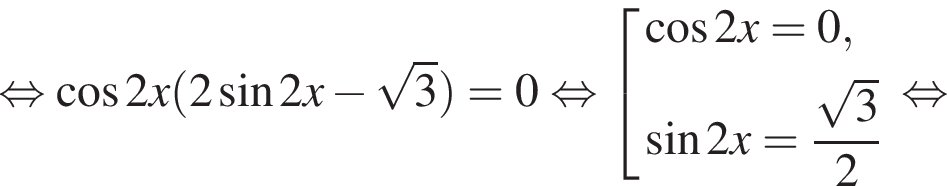
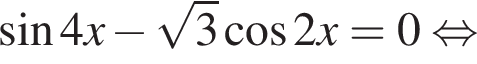

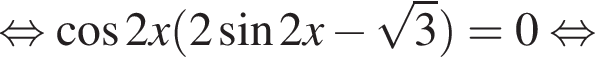
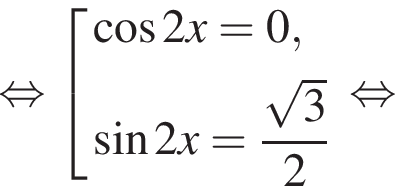
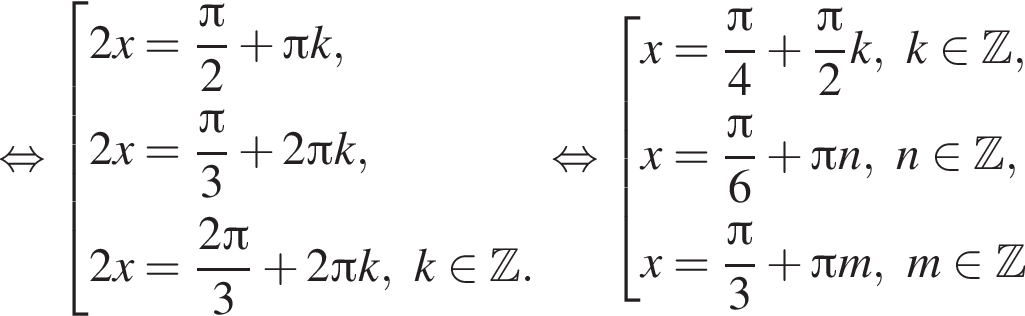
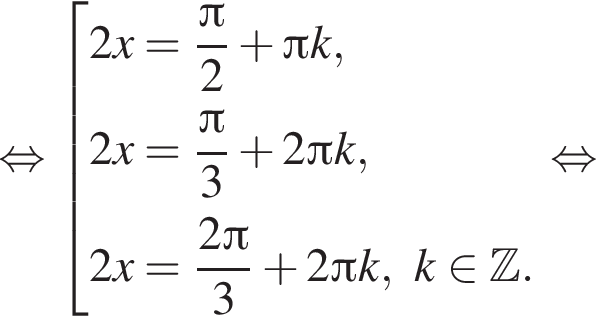
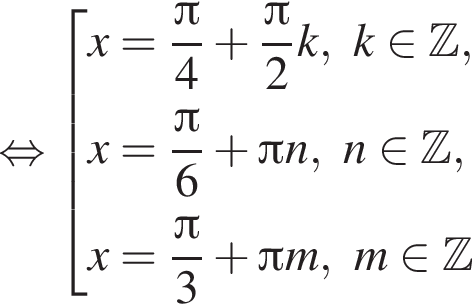
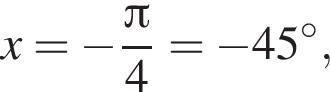 наименьшим положительным решением уравнения является корень
наименьшим положительным решением уравнения является корень 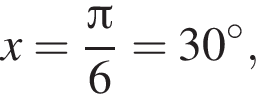 их сумма равна −15°.
их сумма равна −15°.
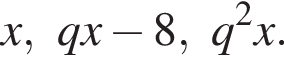
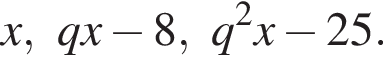
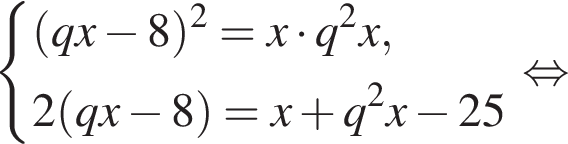
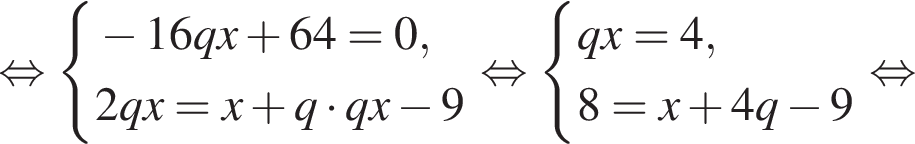
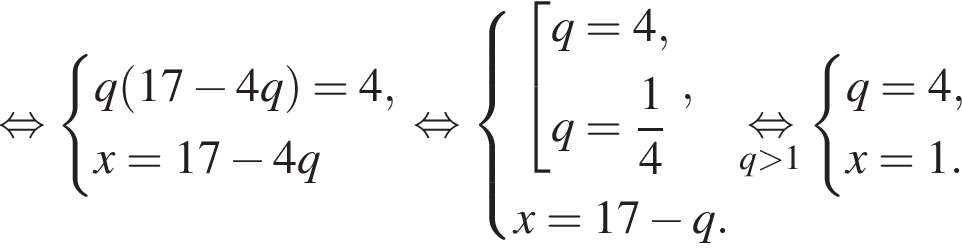
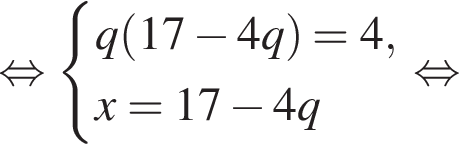
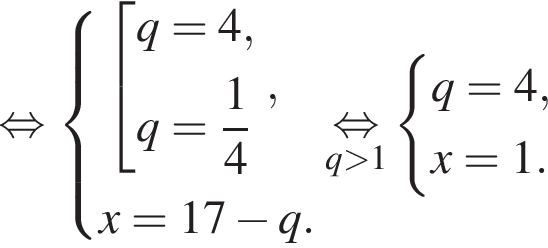
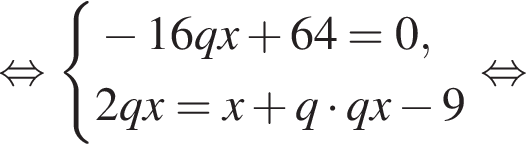
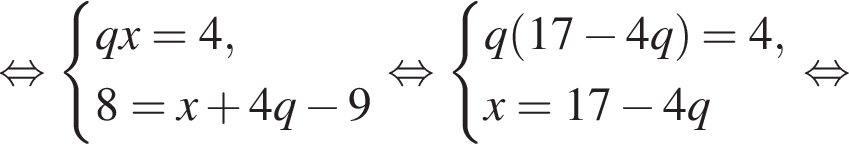
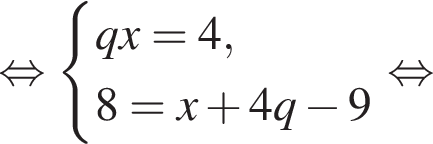
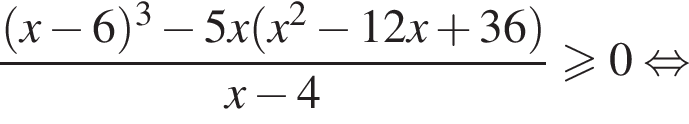
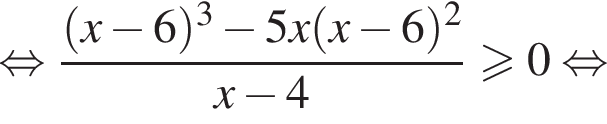
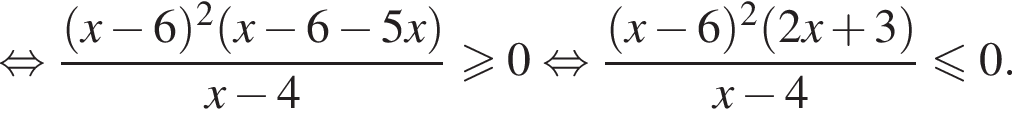
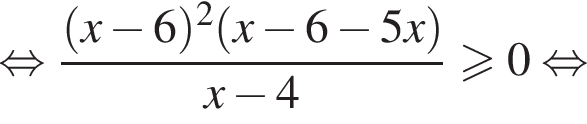
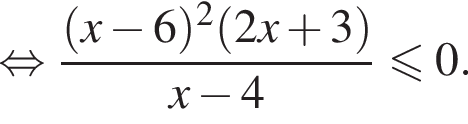
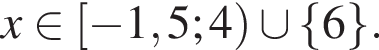 Целыми решениями неравенства являются числа −1, 0, 1, 2, 3, 6. Их сумма равна 11.
Целыми решениями неравенства являются числа −1, 0, 1, 2, 3, 6. Их сумма равна 11.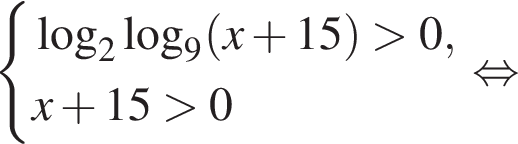
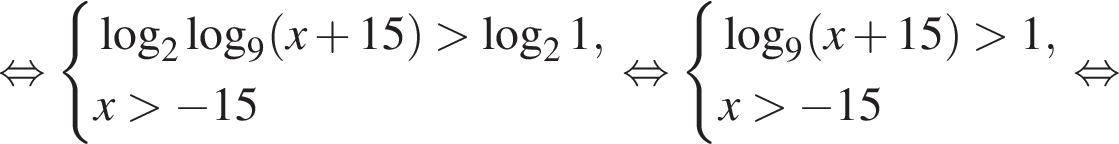
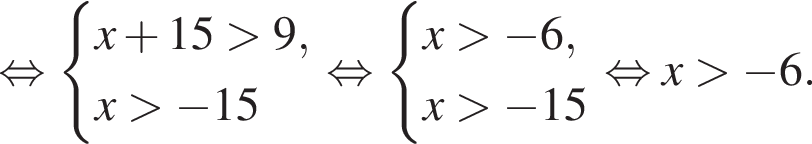
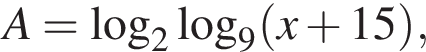 тогда:
тогда: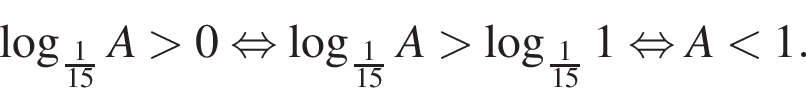
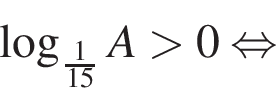
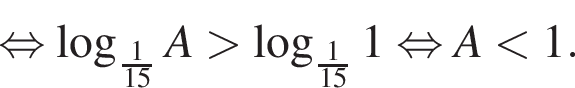

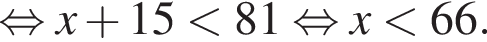


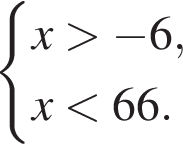 Поэтому наибольшее целое значение — 65, наименьшее целое значение −5, их сумма равна 60.
Поэтому наибольшее целое значение — 65, наименьшее целое значение −5, их сумма равна 60.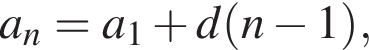 где d — разность арифметической прогрессии.
где d — разность арифметической прогрессии. 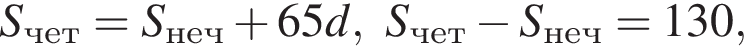 откуда
откуда 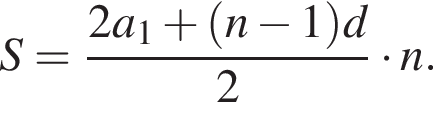 Следовательно, согласно условию, имеем:
Следовательно, согласно условию, имеем: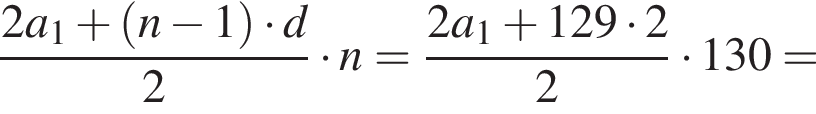
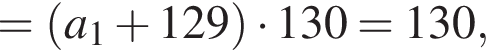
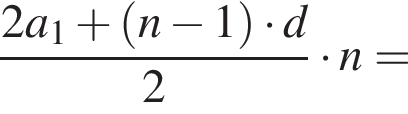
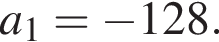 Получим
Получим 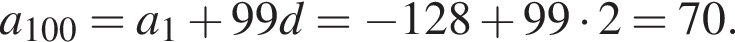
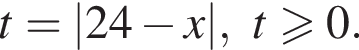 Имеем:
Имеем: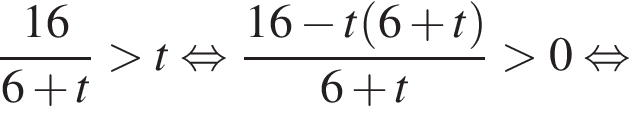
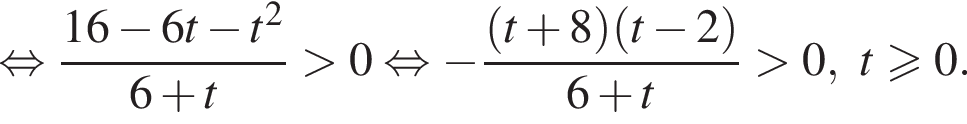
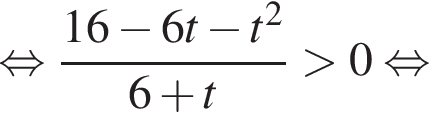
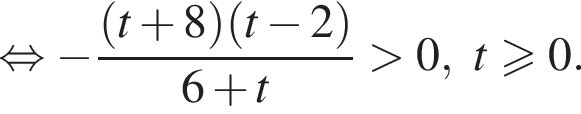
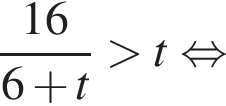
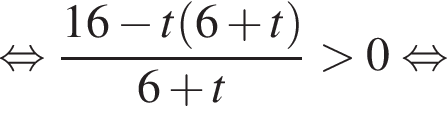
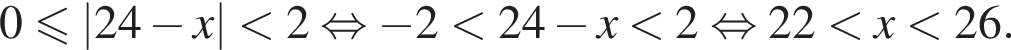
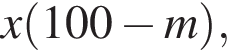 во втором —
во втором — 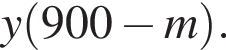 После переливания масса спирта в 1-ом сосуде равна
После переливания масса спирта в 1-ом сосуде равна 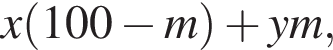 во втором —
во втором —  Так как концентрации стали одинаковыми, а объёмы относятся как 1:9, во втором сосуде в 9 раз больше спирта. Тогда:
Так как концентрации стали одинаковыми, а объёмы относятся как 1:9, во втором сосуде в 9 раз больше спирта. Тогда: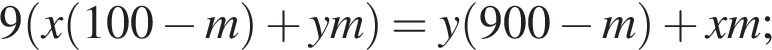
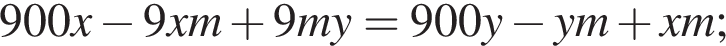

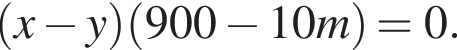

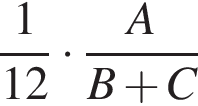 работы.
работы. 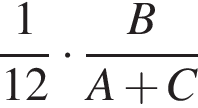 работы.
работы. 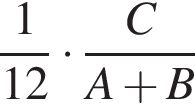 работы.
работы. 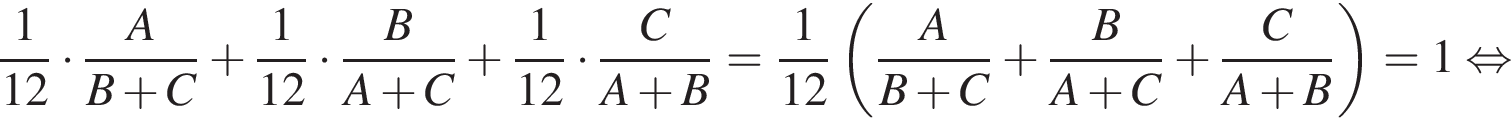
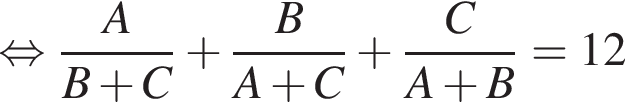
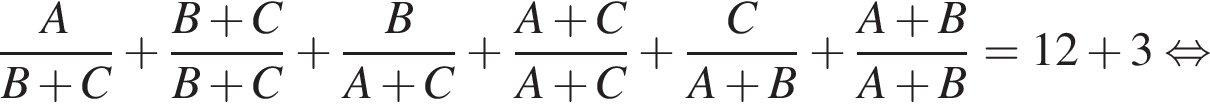
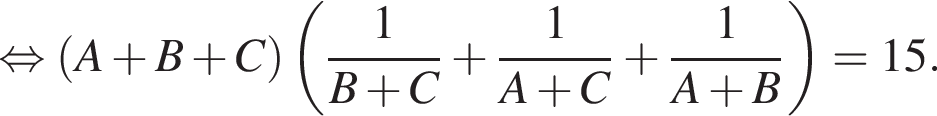
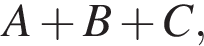 то они выполнили бы работу за:
то они выполнили бы работу за: 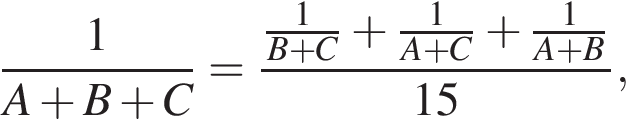
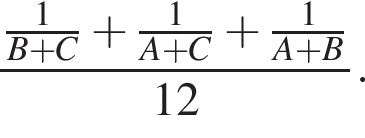 Поэтому, работая вместе работа была бы выполнена в
Поэтому, работая вместе работа была бы выполнена в 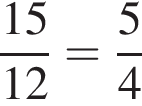 раза быстрее. В ответе будет число
раза быстрее. В ответе будет число 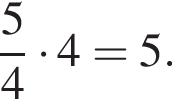
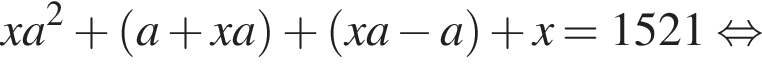
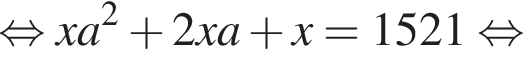

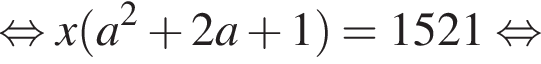
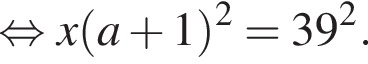
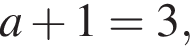
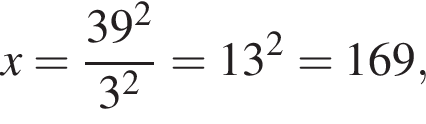
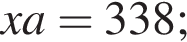
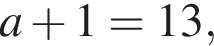
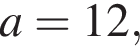
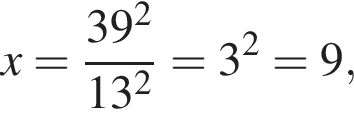
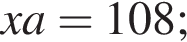
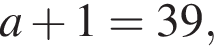
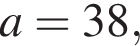
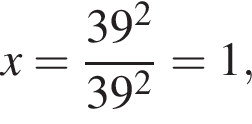
 что запрещено по условию.
что запрещено по условию.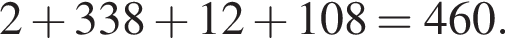
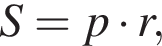 где p — полупериметр. Находим:
где p — полупериметр. Находим: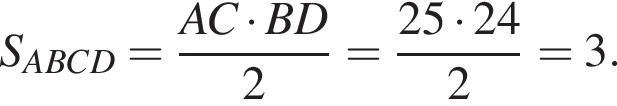
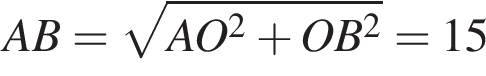 и
и 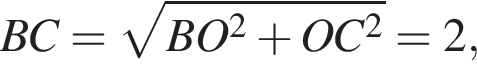 следовательно,
следовательно,